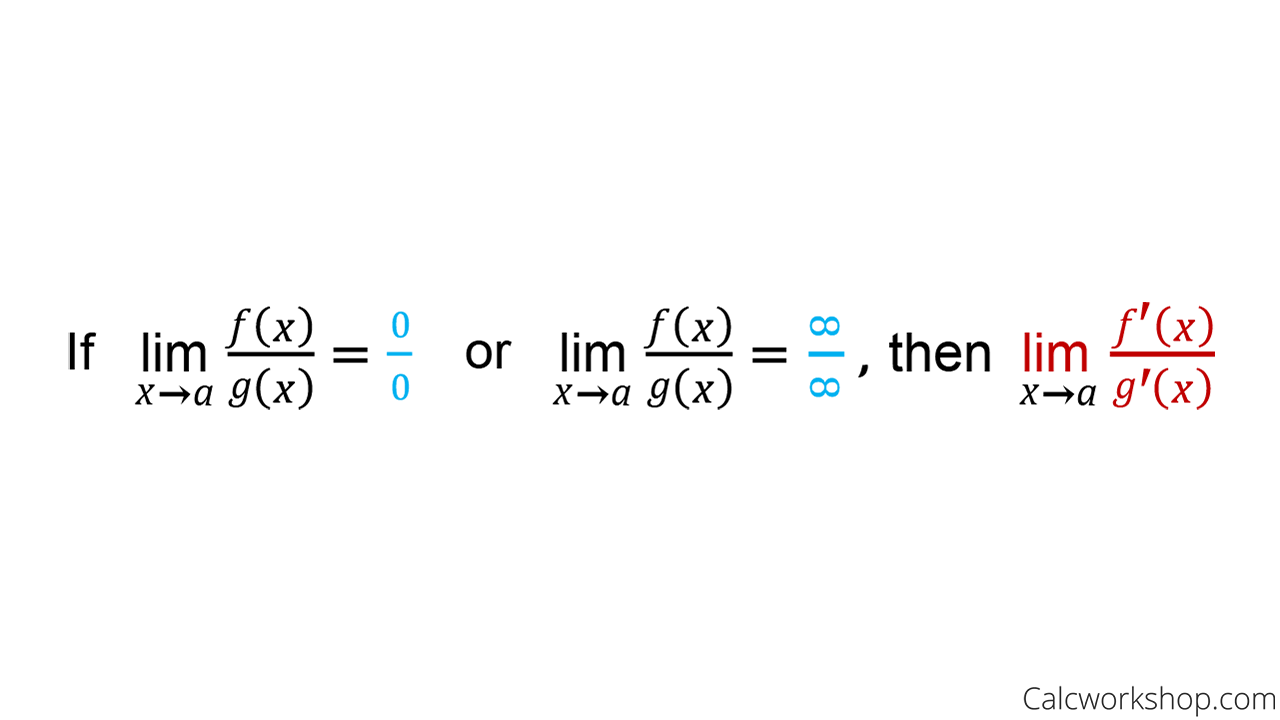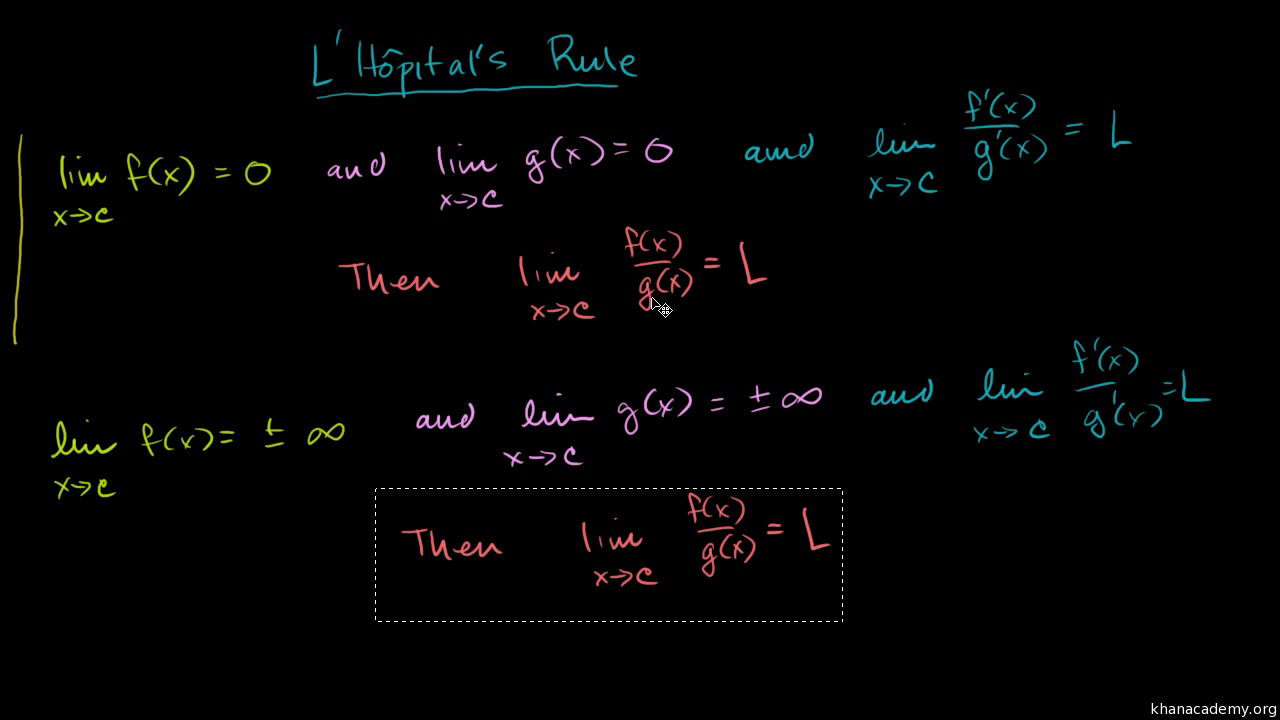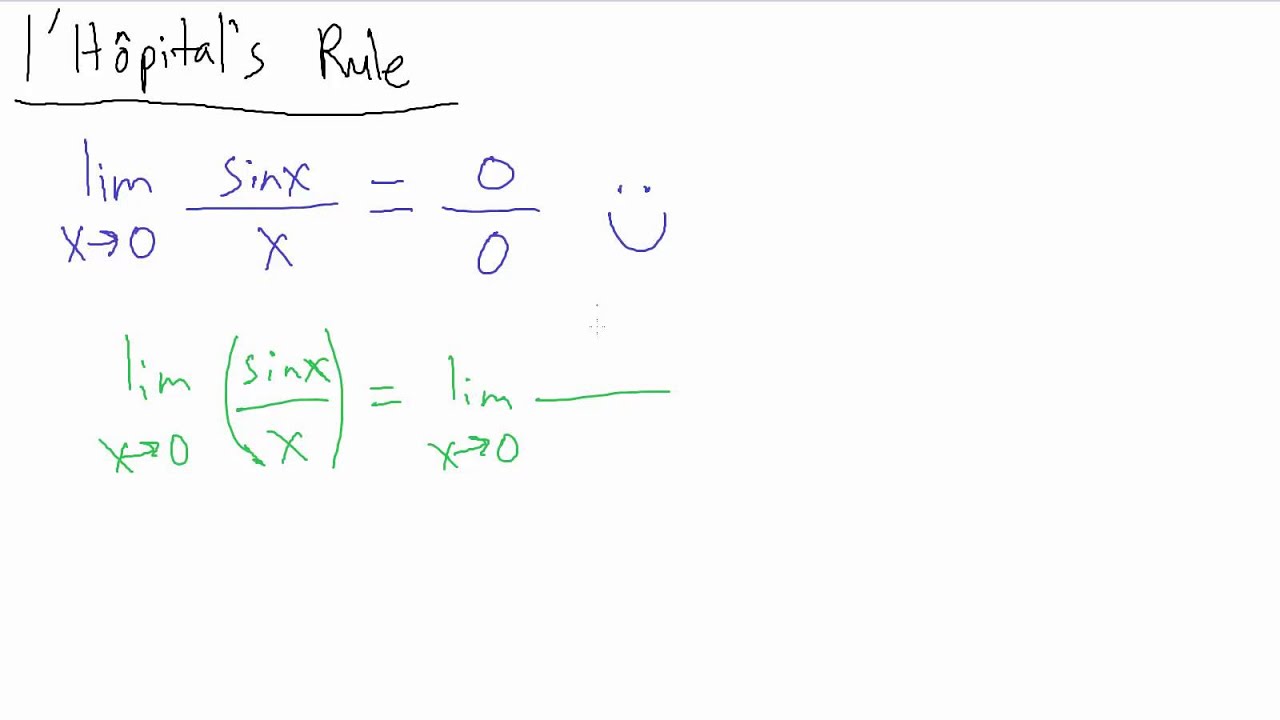L Hopitals Rule

Let lim stand for the limit or and suppose that lim and lim are both zero or are both.

L hopitals rule. It is named for the french mathematician guillaume françois antoine marquis de l hôpital who purchased the formula from his teacher the swiss mathematician johann bernoulli. It involves taking the derivatives of these limits which can simplify the evaluation of the limit. And in this case you can neither use algebraic manipulation nor rearrangement of terms to reduce this expression into a form that yields a valid limit. In both forms of l hopital s rule it should be noted that you are required to differentiate separately the numerator and denominator of the ratio if either of the indeterminate forms frac 0 0 or frac infty infty arises in the computation of a limit.

The theorem states that if f and g are differentiable and g x 0 on an open interval containing a except possibly at a and one of the following holds. Before proceeding with examples let me address the spelling of l hospital. Lopital provides a technique to evaluate limits of indeterminate forms. Within the book l hospital thanks the bernoulli brothers for their assistance and their discoveries.

Application or repeated application of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. This proof is taken from salas and hille s. L hôpital is pronounced lopital who was a french mathematician from the 1600s. The case x to c can be proven in a similar manner and these two cases together can be used to prove l hôpital s rule for a two sided limit.

So l hospital s rule tells us that if we have an indeterminate form 0 0 or all we need to do is differentiate the numerator and differentiate the denominator and then take the limit. 1 has a finite value or if the limit is then. Under certain circumstances we can use a powerful theorem called l hôpital s rule to evaluate the limits that lead to indeterminate forms. L hopital s rule is a theorem that can be used to evaluate difficult limits.

The more modern spelling is l hôpital. In mathematics more specifically calculus l hôpital s rule or l hospital s rule french. We will now sketch the proof of l hôpital s rule for the frac 0 0 case in the limit as x to c where c is finite. 2 historically this result first appeared in l hospital s 1696 treatise which was the first textbook on differential calculus.

Direct substitution tells us that the answer is 1 2. It says that the limit when we divide one function by another is the same after we take the derivative of each function with some special conditions shown later. L hôpital s rule can only be applied in the case where direct substitution yields an indeterminate form meaning 0 0 or. Think about the limit of x 1 x 2 as x approaches 0.